/Szkoła średnia/Liczby/Wyrażenia algebraiczne

Zadanie nr 2492849

Dodaj do ulubionych
Dodaj do rozwiązanych

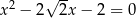Liczba a jest dodatnim pierwiastkiem równania 2 √ -- x − 2 2x − 2 = 0 . Oblicz wartość wyrażenia

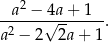
2 -a--−-4√a-+-1--. a2 − 2 2a+ 1

Rozwiązanie

Rozwiązujemy najpierw podane równanie kwadratowe.

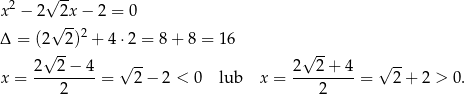
2 √ -- x − 2 √2x-− 2 = 0 Δ = (2 2)2 + 4⋅ 2 = 8+ 8 = 16 √ -- √ -- 2--2−--4- √ -- 2--2-+-4- √ -- x = 2 = 2 − 2 < 0 lub x = 2 = 2 + 2 > 0.

Zatem 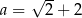√ -- a = 2 + 2 . Skorzystamy teraz ze wzoru skróconego mnożenia

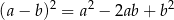
2 2 2 (a− b) = a − 2ab + b

na kwadrat różnicy. Mamy zatem

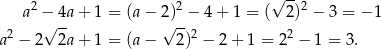
2 2 √ --2 a − 4a+ 1 = (a − 2) − 4+ 1 = ( 2) − 3 = − 1 2 √ -- √ --2 2 a − 2 2a+ 1 = (a − 2) − 2+ 1 = 2 − 1 = 3.

Stąd

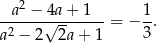
2 --a-−-√4a+--1--= − 1. a2 − 2 2a + 1 3

Mogliśmy też odrobinę skrócić ten rachunek i zauważyć, że

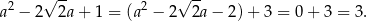
√ -- √ -- a2 − 2 2a+ 1 = (a2 − 2 2a − 2) + 3 = 0 + 3 = 3.

 
Odpowiedź: 1 − 3

Wersja PDF