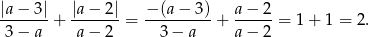Zadanie nr 2832612
Wykaż, że dla 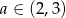 zachodzi równość
zachodzi równość 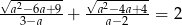 .
.
Rozwiązanie
Chwilkę się przyglądamy i zauważamy, że pod pierwiastkami mamy pełne kwadraty.
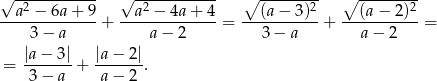
Teraz nadeszła pora na skorzystanie z założenia 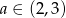 . Dzięki temu założeniu wiemy, że
. Dzięki temu założeniu wiemy, że 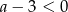 oraz
oraz 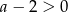 . Zatem
. Zatem
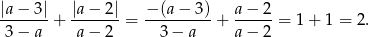
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla 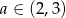 zachodzi równość
zachodzi równość 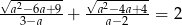 .
.
Chwilkę się przyglądamy i zauważamy, że pod pierwiastkami mamy pełne kwadraty.
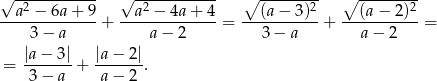
Teraz nadeszła pora na skorzystanie z założenia 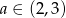 . Dzięki temu założeniu wiemy, że
. Dzięki temu założeniu wiemy, że 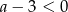 oraz
oraz 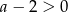 . Zatem
. Zatem