Zadanie nr 2911398
Udowodnij, że jeżeli 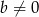 i
i 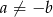 , to
, to 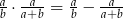 .
.
Rozwiązanie
Sposób I
Jest jasne, że jeżeli 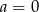 , to dana równość jest spełniona, więc załóżmy, że
, to dana równość jest spełniona, więc załóżmy, że 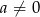 . Przekształcamy daną równość w sposób równoważny.
. Przekształcamy daną równość w sposób równoważny.
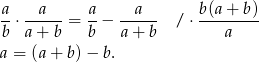
Otrzymana równość jest oczywiście spełniona, więc wyjściowa też musiała być spełniona (bo przekształcaliśmy ją w sposób równoważny).
Sposób II
Przekształcamy prawą stronę danej równości.
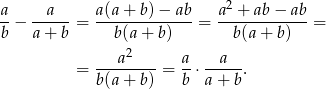
Sposób III
Przekształcamy daną równość w sposób równoważny.
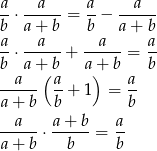
Otrzymana równość jest oczywiście spełniona, więc wyjściowa też musiała być spełniona (bo przekształcaliśmy ją w sposób równoważny).

