Zadanie nr 3751609
Udowodnij, że jeżeli liczba 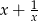 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 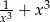 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Rozwiązanie
Niech 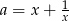 będzie liczbą całkowitą. Wtedy
będzie liczbą całkowitą. Wtedy
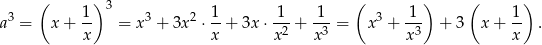
To oczywiście oznacza, że
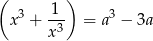
też jest liczbą całkowitą.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że jeżeli liczba 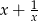 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 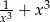 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Niech 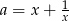 będzie liczbą całkowitą. Wtedy
będzie liczbą całkowitą. Wtedy
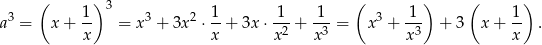
To oczywiście oznacza, że
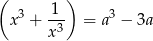
też jest liczbą całkowitą.
