Zadanie nr 4257109
Wykaż, że jeżeli liczby rzeczywiste 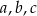 spełniają warunek
spełniają warunek  , to
, to
Rozwiązanie
Podstawmy 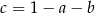 w lewej stronie równości, którą mamy udowodnić.
w lewej stronie równości, którą mamy udowodnić.
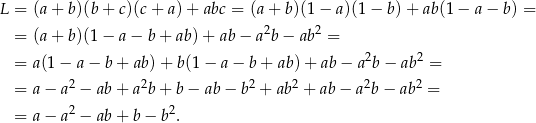
To samo robimy z prawą stroną.
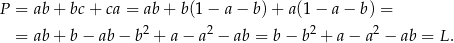
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli liczby rzeczywiste 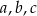 spełniają warunek
spełniają warunek  , to
, to
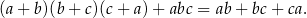
Podstawmy 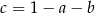 w lewej stronie równości, którą mamy udowodnić.
w lewej stronie równości, którą mamy udowodnić.
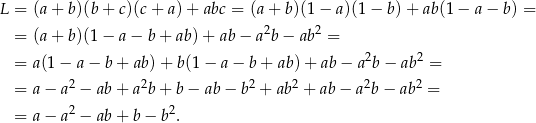
To samo robimy z prawą stroną.