Zadanie nr 4425743
Wykaż, że jeżeli liczby 
i 
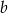spełniają równość 
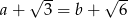to przynajmniej jedna z nich jest niewymierna.
Rozwiązanie
Załóżmy przeciwnie, że obie liczby są wymierne. Mamy wtedy.
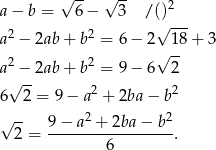
To jednak oznacza, że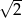 
jest liczbą wymierną, co stanowi sprzeczność. Otrzymana sprzeczność oznacza, że liczby 
i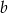 
nie mogą być obie wymierne.
