Zadanie nr 4838925
Wykaż, że jeżeli 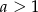 i
i 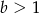 oraz
oraz 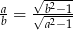 to
to 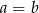 .
.
Rozwiązanie
Przekształcamy w sposób równoważny podaną równość
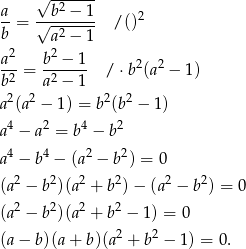
Teraz wystarczy zauważyć, że, na mocy założenia 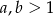 , wyrażenia w drugim i trzecim nawiasie są dodatnie, czyli zerowe musi być wyrażenie w pierwszym nawiasie, co dowodzi, że
, wyrażenia w drugim i trzecim nawiasie są dodatnie, czyli zerowe musi być wyrażenie w pierwszym nawiasie, co dowodzi, że 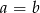 .
.

