/Szkoła średnia/Liczby/Wyrażenia algebraiczne

Zadanie nr 8243190

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że jeżeli liczby niezerowe 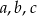a,b,c spełniają warunek 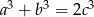3 3 3 a + b = 2c to

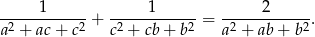
-----1------+ -----1------= -----2------. a2 + ac + c2 c2 + cb + b2 a2 + ab+ b2

Rozwiązanie

Zauważmy najpierw, że jeżeli któreś dwie spośród liczb 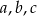a ,b,c są równe, to z warunku 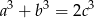a3 + b3 = 2c3 wynika, że 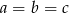a = b = c i równość, którą mamy udowodnić jest oczywista. Załóżmy zatem, że żadne dwie spośród liczb 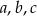a,b,c nie są równe.

Zauważmy, że każdy z mianowników to ’prawie’ wzór na różnicę sześcianów. Spróbujmy to wykorzystać.

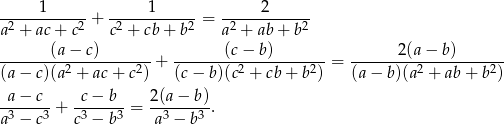
1 1 2 -2--------2-+ 2---------2-= -2---------2 a + ac + c c + cb + b a + ab+ b ------(a-−-c)-------- -------(c-−-b)------- -------2(a-−-b)------ (a− c)(a 2 + ac + c2) + (c − b)(c2 + cb+ b2) = (a − b)(a 2 + ab + b2) -a−-c--+ -c−-b--= 2(a-−-b). a3 − c3 c3 − b3 a3 − b3

Sposób I

Korzystamy teraz z podanego warunku. Jeżeli oznaczymy 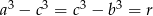a3 − c3 = c3 − b3 = r to

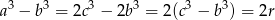
a3 − b3 = 2c3 − 2b3 = 2(c3 − b 3) = 2r

i mamy

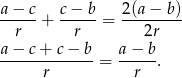
a− c c− b 2(a − b) -----+ -----= --------- r r 2r a−-c-+-c-−-b-= a−--b. r r

Otrzymana równość jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.

Sposób II

Zauważmy, że podany warunek możemy zapisać w postaci 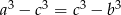a3 − c3 = c3 − b3 . Mamy zatem

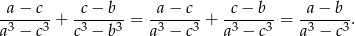
-a−--c- -c−--b- -a-−-c- -c-−-b- -a−--b- a3 − c3 + c3 − b3 = a3 − c3 + a3 − c3 = a3 − c3.

Pozostało więc udowodnić, że

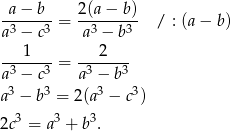
-a-−-b- 2(a−--b)- a3 − c3 = a 3 − b3 / : (a− b) 1 2 ------- = ------- a3 − c3 a3 − b3 a3 − b3 = 2(a3 − c3) 3 3 3 2c = a + b .

Otrzymana równość jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.

Sposób III

Przekształcamy lewą stronę równości podstawiając 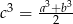c3 = a3+b-3 2 .

-a-−-c- -c-−-b- --a-−-c--- --c-−-b--- L = a3 − c3 + c3 − b3 = 3 a3+b-3+ a3+b3 3 = a − 2 2 − b 2(a-−-c) 2-(c−-b)- 2(a-−-b)- = a3 − b3 + a3 − b3 = a3 − b3 = P.
Wersja PDF