Zadanie nr 9394468
Wykaż, że jeżeli liczby rzeczywiste 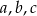 spełniają warunek
spełniają warunek 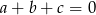 , to
, to
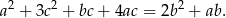
Rozwiązanie
Przekształcamy lewą stronę równości, którą mamy udowodnić tak, aby otrzymać prawą stronę. W tym celu podstawiamy w wyrażeniu z lewej strony 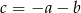 .
.
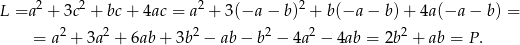
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli liczby rzeczywiste 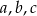 spełniają warunek
spełniają warunek 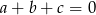 , to
, to
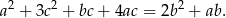
Przekształcamy lewą stronę równości, którą mamy udowodnić tak, aby otrzymać prawą stronę. W tym celu podstawiamy w wyrażeniu z lewej strony 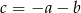 .
.