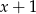/Szkoła średnia/Liczby/Wyrażenia algebraiczne

Zadanie nr 9832001

Dodaj do ulubionych
Dodaj do rozwiązanych

Uprość wyrażenie 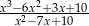x3−6x2+3x+10- x2−7x+10 .

Rozwiązanie

Rozłożymy licznik i mianownik na czynniki. Najpierw licznik: szukamy pierwiastków całkowitych wśród dzielników wyrazu wolnego. Łatwo znaleźć pierwiastek 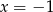x = − 1 . Dzielimy zatem wielomian przez 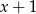x + 1 – my zrobimy to grupując wyrazy.

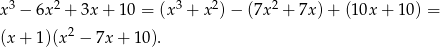
x3 − 6x2 + 3x + 10 = (x3 + x2)− (7x2 + 7x) + (10x + 10 ) = 2 (x + 1)(x − 7x + 10).

No i dalej nie ma co liczyć, bo wyrażenie w nawiasie to mianownik wyjściowego ułamka.

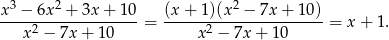
x3 − 6x2 + 3x + 10 (x + 1)(x2 − 7x + 10) -------------------= ----------------------= x + 1. x2 − 7x+ 10 x 2 − 7x + 10

 
Odpowiedź: x + 1

Wersja PDF