Zadanie nr 4128274
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 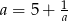 , to
, to 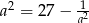 .
.
Rozwiązanie
Sposób I
Przekształcamy daną równość
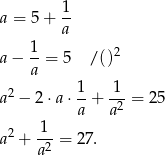
Sposób II
Spróbujmy przekształcić równość, którą mamy uzasadnić
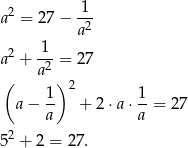
Otrzymana równość jest prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.

