Zadanie nr 9613228

Uzasadnij, że dla dowolnej liczby naturalnej 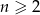n ≥ 2 spełniona jest równość

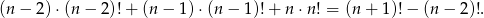
(n− 2)⋅ (n− 2)!+ (n − 1 )⋅(n − 1)!+ n ⋅n! = (n + 1)!− (n− 2)!.

Wersja PDF

Rozwiązanie

Sposób I

Zauważmy, że składnik 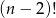(n− 2)! pojawia się w tej równości dwa razy – potraktujmy to jako punkt zaczepienia.

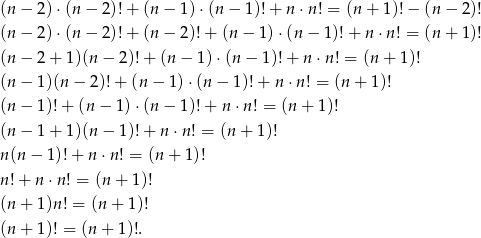
(n − 2) ⋅(n − 2)!+ (n− 1)⋅(n − 1)!+ n ⋅n! = (n + 1 )! − (n − 2)! (n − 2) ⋅(n − 2)!+ (n− 2)!+ (n − 1 )⋅(n − 1)!+ n ⋅n! = (n + 1)! (n − 2 + 1)(n − 2)! + (n − 1) ⋅(n− 1)!+ n ⋅n ! = (n+ 1)! (n − 1)(n − 2)! + (n − 1) ⋅(n − 1)!+ n⋅n ! = (n+ 1)! (n − 1)!+ (n− 1)⋅ (n− 1)!+ n ⋅n ! = (n + 1)! (n − 1 + 1)(n − 1)! + n ⋅n! = (n + 1)! n(n − 1 )!+ n ⋅n! = (n + 1)! n!+ n ⋅n! = (n + 1)! (n + 1)n ! = (n + 1)! (n + 1)! = (n + 1)!.

Otrzymaliśmy równość prawdziwą, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.

Sposób II

Tym razem będziemy rozpisywać silnie pozbywając się po kolei największych z nich. Zaczynamy od 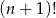(n + 1 )! .

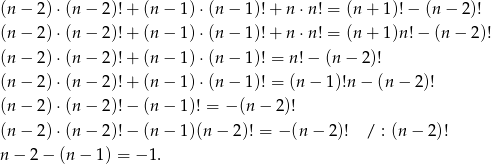
(n − 2 )⋅(n − 2)! + (n − 1) ⋅(n − 1)!+ n ⋅n ! = (n+ 1)!− (n − 2 )! (n − 2 )⋅(n − 2)! + (n − 1) ⋅(n − 1)!+ n ⋅n ! = (n+ 1)n!− (n− 2)! (n − 2 )⋅(n − 2)! + (n − 1) ⋅(n − 1)! = n!− (n− 2)! (n − 2 )⋅(n − 2)! + (n − 1) ⋅(n − 1)! = (n − 1)!n − (n − 2)! (n − 2 )⋅(n − 2)! − (n − 1)! = − (n − 2)! (n − 2 )⋅(n − 2)! − (n − 1)(n − 2)! = − (n − 2)! / : (n− 2)! n − 2 − (n − 1) = − 1.

Otrzymaliśmy równość prawdziwą, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.

Sposób III

Tym razem od razu pozbędziemy się silni dzieląc obie strony równości przez 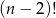(n − 2)! .

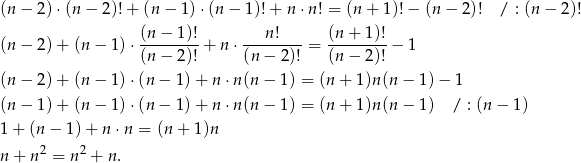
(n − 2)⋅ (n− 2)!+ (n − 1 )⋅(n − 1)! + n ⋅n! = (n + 1)!− (n − 2)! / : (n − 2 )! (n-−-1)! ---n!--- (n+--1)! (n − 2)+ (n − 1) ⋅(n − 2)! + n ⋅(n − 2)! = (n− 2)! − 1 (n − 2)+ (n − 1) ⋅(n− 1)+ n⋅ n(n − 1) = (n + 1 )n(n − 1) − 1 (n − 1)+ (n − 1) ⋅(n− 1)+ n⋅ n(n − 1) = (n + 1 )n(n − 1) / : (n − 1) 1+ (n − 1)+ n ⋅n = (n + 1)n n + n2 = n 2 + n .

Otrzymaliśmy równość prawdziwą, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.