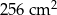/Szkoła podstawowa/Geometria/Czworokąty/Trapez

Zadanie nr 2458628

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

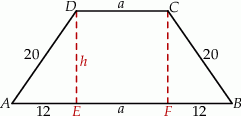
Zauważmy, że różnica podstaw trapezu to

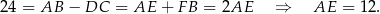
24 = AB − DC = AE + F B = 2AE ⇒ AE = 12 .

Jeżeli oznaczymy 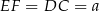EF = DC = a to z podanego obwodu mamy równanie

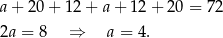
a+ 2 0+ 12+ a+ 12+ 20 = 72 2a = 8 ⇒ a = 4.

Korzystając z twierdzenia Pitagorasa obliczamy wysokość trapezu.

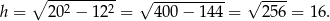
∘ ---------- √ ---------- √ ---- h = 202 − 122 = 4 00− 144 = 25 6 = 16.

Obliczamy pole

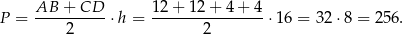
AB--+-CD-- 12-+-12-+-4-+-4- P = 2 ⋅h = 2 ⋅16 = 32⋅ 8 = 256.

 
Odpowiedź: 256 cm 2

Wersja PDF