Zadanie nr 6473745
Karol wyciął z kartonu trójkąt prostokątny 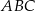 (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
(rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt 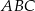 wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez 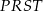 o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
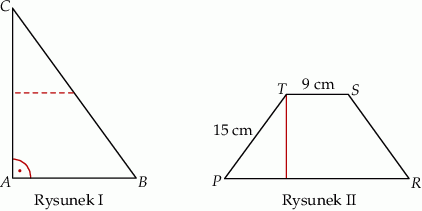
Oblicz różnicę obwodów trójkąta 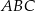 i trapezu
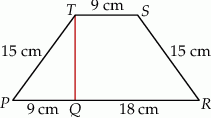
i trapezu 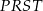 .
.
Rozwiązanie
Obliczamy najpierw wysokość trapezu z rysunku II.
Stosujemy twierdzenie Pitagorasa w trójkącie 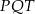 .
.
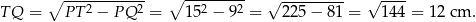
Obwód trójkąta 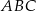 jest więc równy
jest więc równy
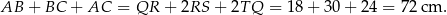
Obwód trapezu jest równy
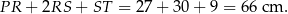
Różnica obwodów tych figur jest równa
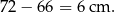
Odpowiedź: 6 cm

