/Szkoła podstawowa/Geometria/Czworokąty/Trapez

Zadanie nr 7460760

Trapez równoramienny 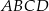ABCD , którego pole jest równe 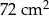2 72 cm , podzielono na trójkąt 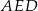AED i trapez 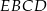EBCD . Odcinek 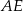AE ma długość równą 4 cm, a odcinek 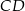CD jest od niego 2 razy dłuższy. Oblicz pole trójkąta AED .

PIC

Wersja PDF

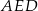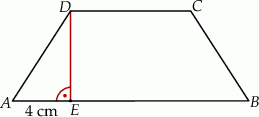
Rozwiązanie

Dorysujmy drugą wysokość trapezu.

PIC

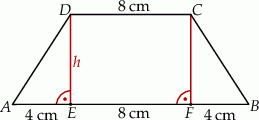
Wiemy, że 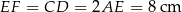EF = CD = 2AE = 8 cm , więc druga podstawa trapezu ma długość

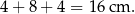
4+ 8+ 4 = 16 cm .

Jeżeli oznaczymy przez 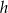h wysokość trapezu, to z podanego pola mamy

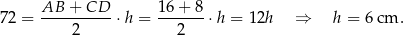
72 = AB--+-CD--⋅h = 16-+-8-⋅h = 1 2h ⇒ h = 6 cm . 2 2

Pole trójkąta 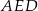AED jest więc równe

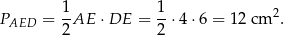
PAED = 1AE ⋅DE = 1-⋅4 ⋅6 = 12 cm 2. 2 2

 
Odpowiedź: 12 cm 2

Wersja PDF