/Szkoła podstawowa/Geometria/Czworokąty/Trapez

Zadanie nr 9839744

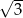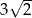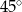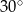Krótsza podstawa trapezu ma długość √ -- 3 , a ramiona długości √ -- 3 2 i 6 tworzą z dłuższą podstawą kąty o miarach 45∘ i 3 0∘ odpowiednio. Oblicz pole trapezu.

Wersja PDF

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

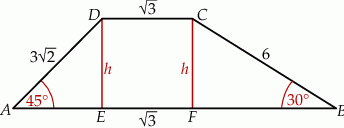
Sposób I

Zauważmy, że trójkąt 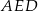AED jest połówką kwadratu o boku 3, więc jego pole jest równe

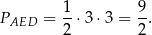
P = 1-⋅3 ⋅3 = 9-. AED 2 2

Ponadto 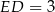ED = 3 i

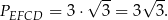
√ -- √ -- PEFCD = 3⋅ 3 = 3 3.

Patrzymy teraz na trójkąt 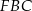FBC – jest to połówka trójkąta równobocznego o boku 6, więc jego pole jest równe

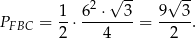
√ -- √ -- 1- 62 ⋅--3 9---3 PFBC = 2 ⋅ 4 = 2 .

Pole trapezu jest więc równe

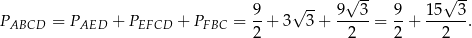
√ -- √ -- √ -- PABCD = PAED + PEFCD + PFBC = 9-+ 3 3+ 9--3-= 9-+ 15---3. 2 2 2 2

Sposób II

Patrzymy najpierw na trójkąt prostokątny 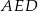AED – możemy z niego obliczyć długości odcinków 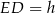ED = h i AE .

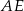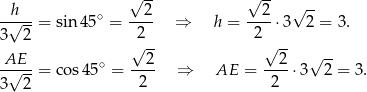
√ -- √ -- √ -- -h√---= sin 45∘ = --2- ⇒ h = --2-⋅3 2 = 3. 3 2 2 2 AE √ 2- √ 2- √ -- -√---= cos45∘ = ---- ⇒ AE = ----⋅3 2 = 3. 3 2 2 2

Podobnie, korzystając z trójkąta 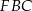F BC obliczamy długość odcinka F B .

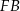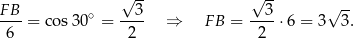
√ -- √ -- FB-= cos 30∘ = --3- ⇒ FB = --3-⋅6 = 3√ 3. 6 2 2

Zatem

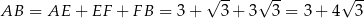
√ -- √ -- √ -- AB = AE + EF + F B = 3 + 3 + 3 3 = 3+ 4 3

i pole trapezu jest równe

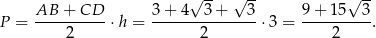
√ -- √ -- √ -- AB--+-CD-- 3-+-4--3-+---3- 9+--15--3- P = 2 ⋅h = 2 ⋅3 = 2 .

 
Odpowiedź: √ - 9 + 15--3 2 2

Wersja PDF