Zadanie nr 2651860

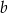Liczby dodatnie i spełniają równość 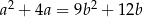2 2 a + 4a = 9b + 12b . Wykaż, że a = 3b .

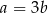Rozwiązanie

Sposób I

Przekształcamy podaną równość (korzystamy ze wzoru skróconego mnożenia na różnicę kwadratów).

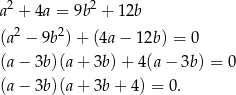
2 2 a + 4a = 9b + 12b (a2 − 9b 2)+ (4a − 12b) = 0 (a− 3b)(a+ 3b)+ 4(a− 3b) = 0 (a− 3b)(a+ 3b+ 4) = 0.

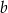Zauważmy teraz, że skoro liczby i są dodatnie, to 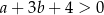a + 3b + 4 > 0 . To oznacza, że a − 3b = 0 .

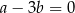Sposób II

Przekształcamy podaną równość (uzupełniamy obie strony do pełnych kwadratów).

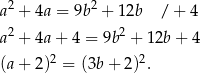
a2 + 4a = 9b 2 + 1 2b / + 4 a2 + 4a + 4 = 9b 2 + 1 2b+ 4 2 2 (a + 2) = (3b + 2) .

Korzystamy teraz ze wzoru skróconego mnożenia na różnicę kwadratów.

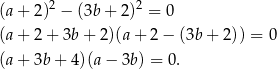
(a+ 2)2 − (3b+ 2)2 = 0 (a+ 2+ 3b+ 2)(a+ 2− (3b+ 2)) = 0 (a+ 3b+ 4)(a− 3b) = 0.

Tak samo jak w poprzednim sposobie wnioskujemy stąd, że 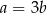a = 3b .

Sposób III

Tak jak w poprzednim sposobie dochodzimy do równości

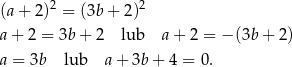
2 2 (a+ 2) = (3b+ 2) a+ 2 = 3b + 2 lub a + 2 = − (3b + 2) a = 3b lub a + 3b + 4 = 0 .

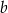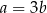Ponieważ liczby i są dodatnie, to druga ewentualność nie jest możliwa. Zatem a = 3b .