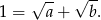Zadanie nr 6826095
Wykaż, że jeżeli 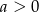 i
i 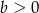 oraz
oraz 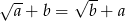 to
to 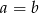 lub
lub 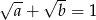 .
.
Rozwiązanie
Przekształcamy podaną równość (korzystamy ze wzoru na różnicę kwadratów)
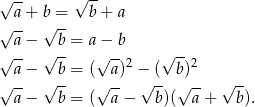
Zatem albo 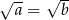 , czyli
, czyli 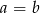 , albo możemy podzielić równość stronami przez
, albo możemy podzielić równość stronami przez 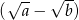 . Mamy wtedy
. Mamy wtedy
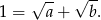
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 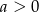 i
i 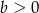 oraz
oraz 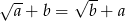 to
to 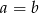 lub
lub 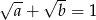 .
.
Przekształcamy podaną równość (korzystamy ze wzoru na różnicę kwadratów)
Zatem albo  , czyli
, czyli  , albo możemy podzielić równość stronami przez
, albo możemy podzielić równość stronami przez  . Mamy wtedy
. Mamy wtedy