Zadanie nr 9520620
Wykaż, że jeżeli 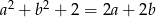 , to
, to 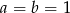 .
.
Rozwiązanie
Przekształcamy równoważnie podaną równość.
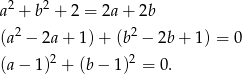
Jeżeli suma kwadratów jest zerem, to zerem muszą być oba składniki, czyli 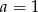 i
i 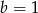 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 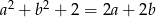 , to
, to 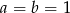 .
.
Przekształcamy równoważnie podaną równość.
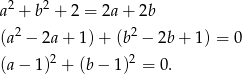
Jeżeli suma kwadratów jest zerem, to zerem muszą być oba składniki, czyli 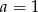 i
i 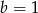 .
.
