Zadanie nr 3810103
Udowodnij, że jeżeli liczby 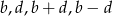 są różne od zera oraz
są różne od zera oraz 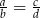 , to
, to 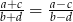 .
.
Rozwiązanie
Wiemy, że
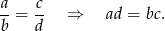
Przekształćmy teraz w sposób równoważny równość, którą mamy udowodnić
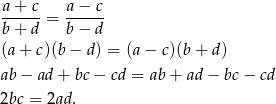
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że jeżeli liczby 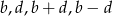 są różne od zera oraz
są różne od zera oraz 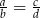 , to
, to 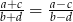 .
.
Wiemy, że
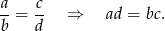
Przekształćmy teraz w sposób równoważny równość, którą mamy udowodnić