/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Udowodnij...

Zadanie nr 1855618

Dodaj do ulubionych
Dodaj do rozwiązanych

Udowodnij, że jeżeli liczby niezerowe 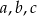a,b,c spełniają warunek 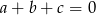a+ b+ c = 0 to

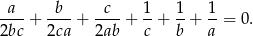
-a--+ -b--+ -c--+ 1-+ 1-+ 1-= 0. 2bc 2ca 2ab c b a

Rozwiązanie

Sposób I

Skorzystamy ze wzoru

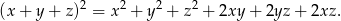
2 2 2 2 (x+ y+ z) = x + y + z + 2xy + 2yz + 2xz .

Przekształcamy lewą stronę równości, którą mamy udowodnić.

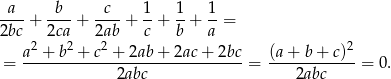
-a--+ -b--+ -c--+ 1-+ 1-+ 1-= 2bc 2ca 2ab c b a a-2 +-b2-+-c2-+-2ab-+-2ac-+-2bc (a-+-b+--c)2 = 2abc = 2abc = 0.

Sposób II

Tak jak poprzednio przekształcamy lewą stronę równości, którą mamy udowodnić do postaci

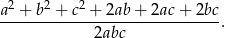
a2 +-b2 +-c2-+-2ab-+-2ac-+-2bc 2abc .

Wystarczy oczywiście teraz udowodnić, że licznik jest równy 0. Zrobimy to podstawiając w wyrażeniu w liczniku 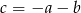c = −a − b .

2 2 2 a + b + c + 2ab + 2ac + 2bc = = a 2 + b2 + (−a − b)2 + 2ab + 2a(−a − b) + 2b(−a − b) = 2 2 2 2 2 2 = a + b + a + 2ab + b + 2ab − 2a − 2ab − 2ab − 2b = 0.
Wersja PDF