/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Udowodnij...

Zadanie nr 3965629

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma dwóch liczb jest równa 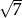√ -- 7 , a ich różnica jest równa 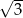√ -- 3 . Wykaż, że iloczyn tych liczb jest liczbą całkowitą.

Rozwiązanie

Sposób I

Mamy układ równań

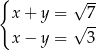
{ √ -- x + y = 7 x − y = √ 3-

Dodajemy równania stronami i mamy

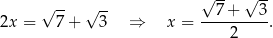
√ -- √ -- √ -- √ -- 2x = 7+ 3 ⇒ x = --7+----3. 2

Jeżeli równania odejmiemy, zamiast dodawać, otrzymamy

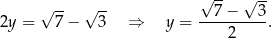
√ -- √ -- √ -- √ -- 2y = 7− 3 ⇒ y = --7−----3. 2

Obliczamy iloczyn tych liczb (korzystamy ze wzoru na różnicę kwadratów)

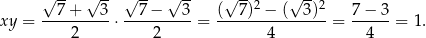
√ -- √ -- √ -- √ -- √ --2 √ -- 2 xy = ---7+---3-⋅ --7−----3-= (---7)-−-(--3-) = 7-−-3-= 1. 2 2 4 4

Oczywiście jest to liczba całkowita.

Sposób II

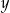Zamiast obliczać x i y mogliśmy skorzystać ze sztuczki

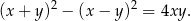
(x+ y)2 − (x− y)2 = 4xy .

Zatem

(x + y )2 − (x − y )2 7 − 4 xy = --------------------= ------= 1. 4 4
Wersja PDF