Zadanie nr 4804993
Wykaż, że dla dowolnych liczb dodatnich  i
i 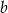 spełniona jest równość
spełniona jest równość
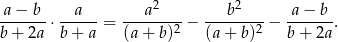
Rozwiązanie
Przekształćmy prawą stronę równości
![2 2 2 2 P = ---a---- − ---b---- − a-−-b--= -a-−--b- − a-−-b--= (a + b)2 (a + b)2 b+ 2a (a + b)2 b+ 2a (a − b)(a + b) a − b a − b a − b = ----------2--- − ------- = ------− -------= (a + b) b + 2a a + b b+ 2a (a-−-b)(b-+-2a)-−-(a-−-b)(a-+-b) = (a+ b)(b+ 2a) = = (a-−-b)[b-+-2a-−-(a+--b)]= ----(a−--b)a----= L. (a+ b)(b+ 2a) (a + b)(b + 2a)](https://img.zadania.info/zad/4804993/HzadR0x.gif)
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych liczb dodatnich  i
i 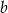 spełniona jest równość
spełniona jest równość
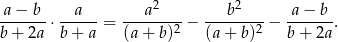
Przekształćmy prawą stronę równości
![2 2 2 2 P = ---a---- − ---b---- − a-−-b--= -a-−--b- − a-−-b--= (a + b)2 (a + b)2 b+ 2a (a + b)2 b+ 2a (a − b)(a + b) a − b a − b a − b = ----------2--- − ------- = ------− -------= (a + b) b + 2a a + b b+ 2a (a-−-b)(b-+-2a)-−-(a-−-b)(a-+-b) = (a+ b)(b+ 2a) = = (a-−-b)[b-+-2a-−-(a+--b)]= ----(a−--b)a----= L. (a+ b)(b+ 2a) (a + b)(b + 2a)](https://img.zadania.info/zad/4804993/HzadR0x.gif)
