Zadanie nr 5923134
Liczby rzeczywiste  i
i 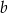 spełniają równość
spełniają równość 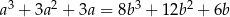 . Wykaż, że
. Wykaż, że 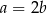 .
.
Rozwiązanie
Sposób I
Przekształcamy podaną równość (korzystamy ze wzorów skróconego mnożenia na różnicę kwadratów i różnicę sześcianów).
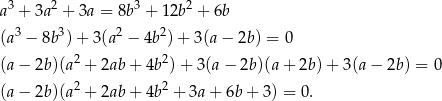
Sprawdzimy teraz, kiedy wyrażenie w drugim nawiasie może być zerem. Potraktujmy to wyrażenie jak funkcję kwadratową zmiennej 
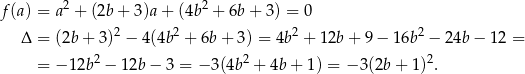
Widzimy, że jedyna możliwość, aby trójmian 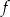 miał pierwiastki, to
miał pierwiastki, to 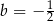 . Wtedy
. Wtedy
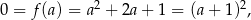
czyli 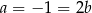 . Jeżeli natomiast
. Jeżeli natomiast 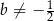 , to
, to
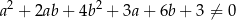
i 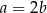 .
.
Sposób II
Przekształcamy podaną równość (uzupełniamy obie strony do pełnych sześcianów).
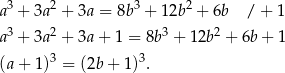
Korzystamy teraz ze wzoru skróconego mnożenia na różnicę sześcianów.
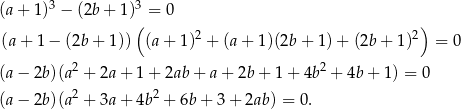
Tak samo jak w poprzednim sposobie wnioskujemy stąd, że 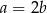 .
.
Sposób III
Tak jak w poprzednim sposobie dochodzimy do równości
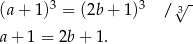
Stąd 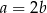 .
.

