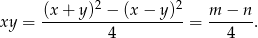/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Udowodnij...

Zadanie nr 9467471

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma dwóch liczb jest równa 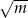√ -- m , a ich różnica jest równa 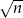√ -- n , gdzie 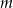m i n są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.

Rozwiązanie

Sposób I

Mamy układ równań

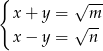
{ √ -- x+ y = √ m- x− y = n

Dodając równania stronami mamy

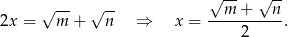
√ -- √ -- √ -- √ -- --m-+---n-- 2x = m + n ⇒ x = 2 .

Jeżeli równania odejmiemy, zamiast dodawać, otrzymamy

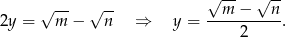
√ -- √ -- √ -- √ -- --m-−---n-- 2y = m − n ⇒ y = 2 .

Liczymy iloczyn tych liczb (korzystamy ze wzoru na różnicę kwadratów)

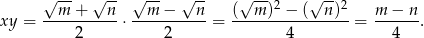
√ -- √ -- √ -- √ -- √ -- √ -- --m-+----n- --m-−----n- (--m-)2-−-(--n-)2 m-−--n xy = 2 ⋅ 2 = 4 = 4 .

Oczywiście jest to liczba wymierna.

Sposób II

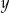Zamiast wyliczać x i y mogliśmy skorzystać ze sztuczki

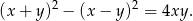
(x+ y)2 − (x− y)2 = 4xy .

Zatem

(x + y)2 − (x − y)2 m − n xy = ---------4----------= --4---.
Wersja PDF