/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Inne

Zadanie nr 9183973

Zaznacz w układzie współrzędnych zbiór wszystkich par 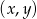(x,y) liczb rzeczywistych, dla których wyrażenie: 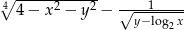∘ ------------ 4 4 − x2 − y2 − √---1---- y−log2x ma wartości rzeczywiste.

Wersja PDF

Rozwiązanie

Sformułowanie zadania jest dość pokrętne, ale nasze zadanie to wyznaczenie dziedziny podanego wyrażenia. Wyrażenie pod pierwszym pierwiastkiem musi być nieujemne, czyli

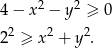
4 − x2 − y2 ≥ 0 2 2 2 2 ≥ x + y .

Punkty spełniające tę nierówność to wnętrze koła o środku 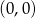(0,0) i promieniu 2.

Wyrażenie pod drugim pierwiastkiem musi być dodatnie (nie może być równe 0, bo jest w mianowniku), czyli

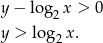
y − log2x > 0 y > log2 x.

Punkty spełniające tę nierówność to punkty leżące powyżej wykresu funkcji 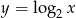y = lo g2x .

Na koniec nie możemy zapomnieć, że musi być 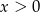x > 0 , ze względu na dziedzinę logarytmu.

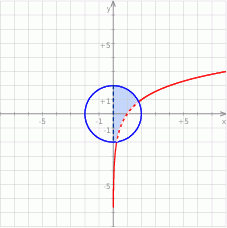
Teraz bez trudu zaznaczamy szukaną dziedzinę.

PIC

Wersja PDF