/Szkoła podstawowa/Geometria/Trójkąt/Równoboczny

Zadanie nr 9787483

Dodaj do ulubionych
Dodaj do rozwiązanych

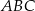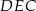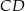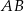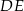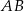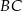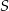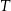Trójkąty ABC i DEC są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki CD i AB są prostopadłe, a odcinek DE przecina odcinki AB i BC w punktach S i T odpowiednio (zobacz rysunek). Oblicz długość odcinka ST .

PIC

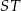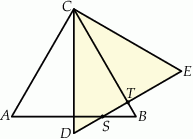
Rozwiązanie

Obliczamy najpierw długość odcinka 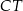CT – jest to wysokość w trójkącie równobocznym CDE .

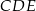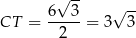
√ -- CT = 6--3-= 3√ 3- 2

(skorzystaliśmy ze wzoru 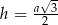√- h = a23- na wysokość trójkąta równobocznego o boku długości a ). W takim razie

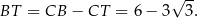
√ -- BT = CB − CT = 6− 3 3.

Trójkąt prostokątny 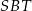SBT ma kąt ostry 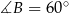∡B = 60∘ , wiec jest to połówka trójkąta równobocznego o boku długości 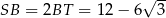SB = 2BT = 12− 6√ 3- . W takim razie

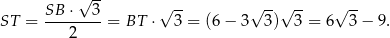
√ -- √ -- √ --√ -- √ -- ST = SB--⋅--3 = BT ⋅ 3 = (6 − 3 3) 3 = 6 3 − 9. 2

 
Odpowiedź: √ -- 6 3 − 9

Wersja PDF