/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki/Inne

Zadanie nr 6182527

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozważmy rzut sześcioma kostkami do gry, z których każda ma inny kolor. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że uzyskany wynik rzutu spełnia równocześnie trzy warunki:
– dokładnie na dwóch kostkach otrzymano po jednym oczku;
– dokładnie na trzech kostkach otrzymano po sześć oczek;
– suma wszystkich otrzymanych liczb oczek jest parzysta.

Rozwiązanie

Za zdarzenia elementarne przyjmujemy ciągi otrzymanych oczek, więc

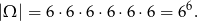
6 |Ω | = 6⋅ 6⋅6 ⋅6 ⋅6⋅ 6 = 6 .

W zdarzeniach elementarnych musimy wybrać dwie kostki, na których ma być jedno oczko, możemy to zrobić na

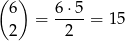
( ) 6 = 6-⋅5 = 1 5 2 2

sposobów. Potem wybieramy 3 kostki, na których ma być 6 oczek – możemy to zrobić na

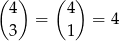
( ) ( ) 4 4 3 = 1 = 4

sposoby. Na koniec na ostatniej kostce musimy wybrać parzystą liczbę oczek (żeby suma na wszystkich kostkach była parzysta), i nie może to być szóstka (bo ma być tylko jedna szóstka) – możemy to zrobić na 2 sposoby. W sumie jest więc

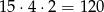
15⋅ 4⋅2 = 120

zdarzeń sprzyjających i prawdopodobieństwo jest równe

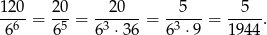
120 20 20 5 5 ----= ---= ------ = ----- = -----. 66 65 63 ⋅ 36 6 3 ⋅9 1944

 
Odpowiedź: 19544

Wersja PDF