/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 26 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Cenę samochodu, który początkowo kosztował 30000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny samochód kosztował
A) 29403 B) 30000 C) 30597 D) 29700
Liczba 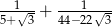 jest liczbą
jest liczbą
A) wymierną B) naturalną C) niewymierną D) większą od 1
O liczbie  wiadomo, że
wiadomo, że 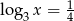 . Zatem
. Zatem
A) 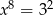 B)
B) 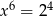 C)
C) 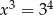 D)
D) 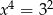
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 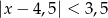 B)
B) 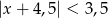 C)
C) 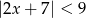 D)
D) 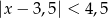
Który z wielomianów należy dodać do wielomianu 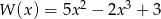 aby otrzymać wielomian
aby otrzymać wielomian 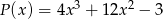 ?
?
A) 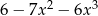 B)
B) 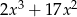 C)
C) 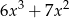 D)
D) 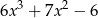
Jeżeli 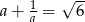 to liczba
to liczba 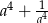 jest równa
jest równa
A) 16 B) 6 C) 14 D) 36
Jeżeli 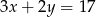 i
i 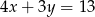 to
to
A) 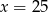 B)
B) 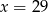 C)
C) 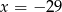 D)
D) 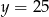
Wierzchołek paraboli będącej wykresem funkcji 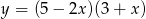 ma współrzędne
ma współrzędne
A) 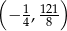 B)
B) 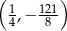 C)
C) 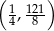 D)
D) 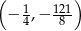
Na rysunku przedstawiono wykres funkcji 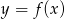 .
.
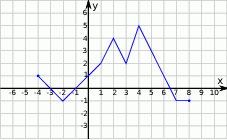
Zbiorem wartości funkcji 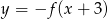 jest
jest
A) 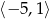 B)
B) 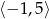 C)
C) 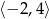 D)
D) 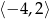
Rozwiązaniem równania 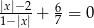 są liczby
są liczby
A) 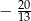 i
i 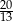 B)
B) 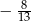 i
i 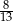 C) -8 i 8 D) -20 i 20
C) -8 i 8 D) -20 i 20
Punkt 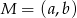 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 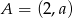 i
i 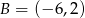 . Wówczas
. Wówczas
A) 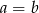 B)
B) 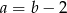 C)
C) 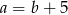 D)
D) 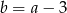
Dwa wyrazy ciągu arytmetycznego o wyrazach całkowitych są równe 319 i 409. Różnica tego ciągu może być równa
A) 12 B) 18 C) 11 D) 19
Dla której z podanych wartości  , wykres funkcji
, wykres funkcji 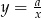 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 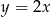 ?
?
A) 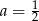 B)
B) 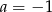 C)
C) 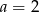 D)
D) 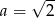
Proste o równaniach 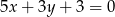 oraz
oraz 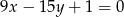
A) są równoległe i różne
B) są prostopadłe
C) przecinają się pod kątem innym niż prosty
D) pokrywają się
Wyrażenie 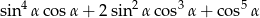 jest równe
jest równe
A) 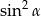 B)
B) 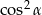 C)
C) 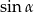 D)
D) 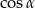
Zbiornik na wodę ma kształt prostopadłościanu o podstawie będącej prostokątem o bokach 5 m i 3 m, oraz o wysokości 4 metrów. Odległość między najdalszymi punktami zbiornika jest
A) większa niż 8 m
B) większa niż 7 m i mniejsza niż 8 m
C) większa niż 6 m i mniejsza niż 7 m
D) większa niż 5 m i mniejsza niż 6 m
Okrąg opisany na sześciokącie foremnym ma promień 2. Promień okręgu wpisanego w ten sześciokąt jest równy
A) 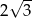 B)
B) 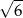 C)
C) 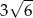 D)
D) 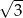
Losujemy jeden wierzchołek i jedną ścianę czworościanu foremnego. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe
A) 1 B) 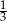 C)
C)  D)
D) 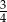
Do wykresu funkcji wykładniczej 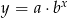 należą punkty
należą punkty 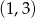 i
i 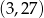 . Zatem liczba
. Zatem liczba 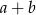 jest równa
jest równa
A) 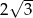 B) 12 C) 4 D)
B) 12 C) 4 D) 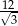
Bok 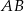 czworokąta
czworokąta 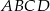 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 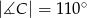 .
.
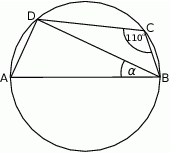
Zatem kąt  ma miarę
ma miarę
A) 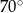 B)
B) 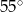 C)
C) 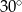 D)
D) 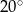
Liczba krawędzi graniastosłupa jest o 10 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 6 B) 18 C) 24 D) 12
Po usunięciu jednej liczby z listy danych: 3,2,4,1,5,1,4,1,5,2 średnia arytmetyczna zwiększyła się o 0,2. Którą liczbę usunięto z listy?
A) 1 B) 2 C) 3 D) 4
Zadania otwarte
Rozwiąż nierówność 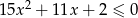 .
.
Oblicz, ile jest liczb naturalnych czterocyfrowych, które są podzielne przez 5, i których zapis składa się z 4 różnych cyfr.
W układzie współrzędnych na płaszczyźnie punkty 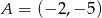 i
i 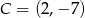 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 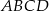 , w którym
, w którym 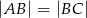 . Wyznacz równanie prostej
. Wyznacz równanie prostej 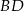 .
.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 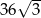 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Obwód trójkąta 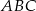 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 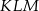 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 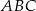 .
.
Punkty 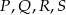 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 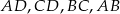 czworościanu
czworościanu 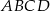 . Wykaż, że punkty
. Wykaż, że punkty 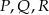 i
i 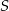 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku.
Wykaż, że jeżeli 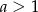 i
i 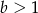 oraz
oraz 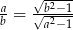 to
to 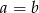 .
.
Jacek wrzucał do skarbonki monety 10 groszowe, przy czym w sumie wrzucił do skarbonki 5,5 zł. Gdyby wrzucał monety ze średnią częstością o 10% większą, to czas potrzebny na wrzucenie wszystkich monet skróciłby się o 5 sekund. Oblicz, ile średnio monet na sekundę wrzucał Jacek do skarbonki.
Oblicz długość cięciwy, którą wycina z prostej 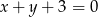 okrąg o środku w punkcie
okrąg o środku w punkcie 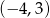 i promieniu 10.
i promieniu 10.
Dla jakich wartości  i
i 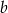 liczby
liczby 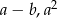 oraz
oraz 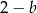 są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?
są trzema kolejnymi wyrazami zarówno ciągu arytmetycznego, jak i geometrycznego?

