/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/Zadania.info

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 5 marca 2011 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Dla jakich wartości parametru 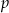p równanie 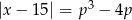3 |x − 1 5| = p − 4p ma dwa rozwiązania, których iloczyn jest liczbą dodatnią?

Zadanie 2
(4 pkt)

Wyznacz dziedzinę funkcji 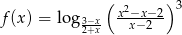( 2 ) 3 f(x) = log 3−x x−xx−-−22- 2+x

Zadanie 3
(3 pkt)

Długości boków trójkąta 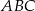ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie 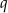q . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 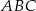ABC są równe miarom kątów trójkąta ABC .

Zadanie 4
(5 pkt)

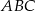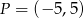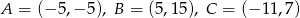Sprawdź czy punkt P = (− 5,5) jest środkiem okręgu wpisanego w trójkąt o wierzchołkach A = (− 5,− 5), B = (5 ,15), C = (− 11,7) .

Zadanie 5
(4 pkt)

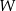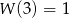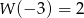Wielomian W jest wielomianem stopnia 5 i spełnia warunki: W (3) = 1 oraz W (− 3) = 2 . Wykaż, że nie wszystkie współczynniki wielomianu 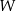W są liczbami całkowitymi.

Zadanie 6
(4 pkt)

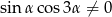Wykaż, że dla dowolnego kąta α takiego, że sinα cos 3α ⁄= 0 zachodzi tożsamość

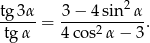
tg3α 3 − 4 sin 2α -----= -----2------. tg α 4 cos α − 3

Zadanie 7
(4 pkt)

Liczby

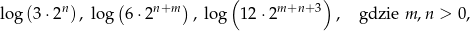
( ) lo g(3 ⋅2n) , log (6⋅ 2n+m ), lo g 12⋅ 2m+n +3 , gdzie m ,n > 0 ,

są odpowiednio pierwszym, piątym i dziewiątym wyrazem ciągu arytmetycznego. Wyznacz różnicę tego ciągu.

Zadanie 8
(6 pkt)

W okrąg o średnicy 26 wpisano trapez równoramienny w ten sposób, że suma kwadratów długości jego podstaw jest równa 914, a sinus kąta ostrego wynosi 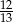12 13 . Oblicz pole tego trapezu.

Zadanie 9
(4 pkt)

Wykaż, że jeżeli punkt 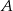A leży na prostej 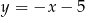y = −x − 5 , a punkt 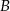B ma współrzędne

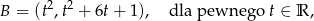
2 2 B = (t ,t + 6t + 1), dla pewnego t ∈ R,

to długość odcinka 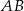AB jest nie mniejsza niż 3√ 2 --4- .

Zadanie 10
(6 pkt)

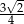W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 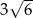√ -- 3 6 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.

Zadanie 11
(5 pkt)

Ile jest liczb naturalnych czterocyfrowych, w których żadne dwie spośród cyfr: 1,3,5,7,9 nie sąsiadują ze sobą?

Arkusz Wersja PDF
Rozwiązania