/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 5 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Cena towaru bez podatku VAT wynosi 180 zł. Ten sam towar wraz z podatkiem VAT i 5% rabatem handlowym kosztuje 184,68 zł. Jaką stawką VAT opodatkowano ten towar?
A) 5% B) 8% C) 23% D) 108%
Przedział 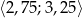 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 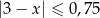 B)
B) 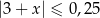 C)
C) 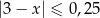 D)
D) 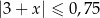
Dane są zbiory 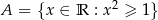 i
i 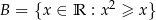 . Zatem zbiór
. Zatem zbiór 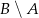 jest równy
jest równy
A) 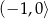 B)
B) 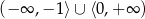
C) 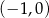 D)
D) 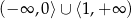
Liczba ![[ ] log4 log36(log√ 28)](https://img.zadania.info/zes/0093759/HzesT12x.gif) jest równa
jest równa
A) 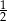 B)
B) 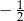 C)
C) 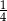 D) 2
D) 2
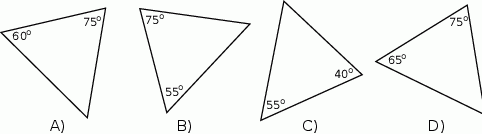
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 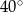 i
i 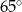 ?
?
Kwadrat liczby 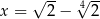 jest równy
jest równy
A) 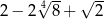 B)
B) 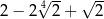 C)
C) 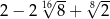 D)
D) 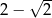
Do zbioru rozwiązań nierówności 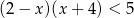 należy liczba
należy liczba
A) 1 B) -2 C) 3 D) -1
Jeden zawór napełnia basen w ciągu 20 minut, a drugi w ciągu 30 minut. W ciągu ilu minut napełnią basen oba zawory odkręcone jednocześnie?
A) 50 B) 25 C) 12 D) 15
Wierzchołek paraboli 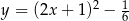 leży na prostej o równaniu
leży na prostej o równaniu
A) 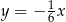 B)
B) 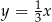 C)
C) 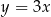 D)
D) 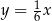
Dziedziną funkcji 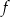 jest przedział
jest przedział 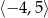 . Poniżej zamieszczono wykres tej funkcji.
. Poniżej zamieszczono wykres tej funkcji.
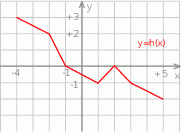
W którym ze zbiorów funkcja 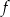 jest malejąca?
jest malejąca?
A) 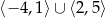 B)
B) 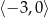 C)
C) 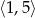 D)
D) 
Zbiór rozwiązań nierówności 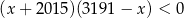 może być przedstawiony na rysunku
może być przedstawiony na rysunku
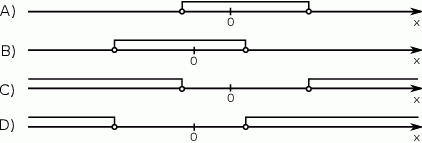
Na którym rysunku przedstawiono wykres funkcji liniowej 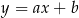 takiej, że
takiej, że 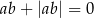 ?
?
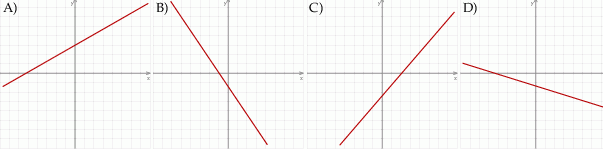
Przedstawiony na rysunku wykres może być wykresem funkcji
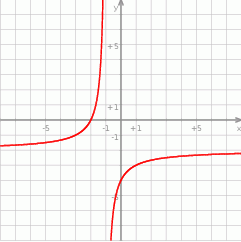
A) 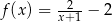 B)
B) 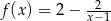 C)
C) 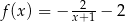 D)
D) 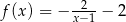
Kwotę 3000 zł wpłacamy do banku na 3 lata. Kapitalizacja odsetek jest dokonywana w tym banku co kwartał, a roczna stopa procentowa wynosi 4%. Po trzech latach otrzymamy kwotę
A) 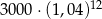 B)
B) 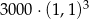 C)
C) 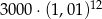 D)
D) 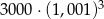
W ciągu arytmetycznym 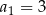 oraz
oraz 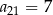 . Wtedy suma
. Wtedy suma 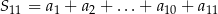 jest równa
jest równa
A) 44 B) 88 C) 46 D) 55
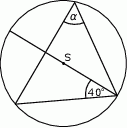
Punkt 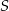 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 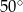 B)
B) 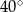 C)
C) 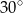 D)
D) 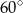
W trójkącie równobocznym 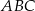 poprowadzono odcinki
poprowadzono odcinki 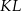 i
i 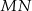 , które podzieliły boki
, które podzieliły boki 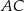 i
i 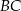 na trzy równe części. Stosunek pola trójkąta
na trzy równe części. Stosunek pola trójkąta 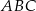 do pola trapezu
do pola trapezu 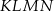 jest równy
jest równy
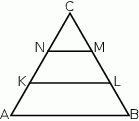
A) 3 B) 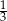 C) 9 D) 6
C) 9 D) 6
Kąt  jest ostry i
jest ostry i 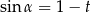 . Wtedy
. Wtedy
A) 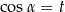 B)
B) 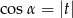 C)
C) 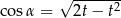 D)
D) 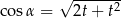
Promień sfery opisanej na sześcianie jest równy 6. Długość krawędzi tego sześcianu jest równa
A) 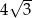 B)
B) 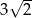 C)
C) 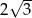 D)
D) 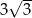
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 1 | 4 | 3 | 5 | 4 | 3 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 4 B) 3,8 C) 3,5 D) 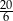
Okrąg o równaniu 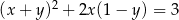 ma promień równy
ma promień równy
A) 3 B) 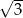 C) 4 D) 2
C) 4 D) 2
Zadania otwarte
Rozwiąż nierówność 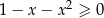 .
.
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.
Proste 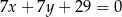 i
i 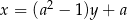 przecinają się pod kątem
przecinają się pod kątem 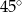 . Wyznacz liczbę
. Wyznacz liczbę  .
.
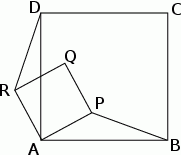
Czworokąty 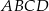 i
i 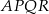 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 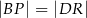 .
.
Wykaż, że liczby 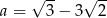 ,
, 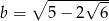 i
i 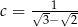 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 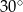 .
.
Trasa rowerowa wokół jeziora ma długość 15 km. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro poruszając się w tym samym kierunku. Średnia prędkość drugiego z nich jest większa od średniej prędkości pierwszego o 5 km/h. Oblicz po jakim czasie dojdzie do ponownego spotkania rowerzystów.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma otrzymanych oczek jest równa co najmniej 5.
Punkty 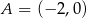 i
i 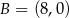 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 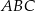 o przeciwprostokątnej
o przeciwprostokątnej 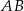 i polu równym 15. Oblicz współrzędne punktu
i polu równym 15. Oblicz współrzędne punktu 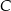 .
.
Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.

