/Szkoła średnia/Zadania maturalne/Matura 2011/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 12 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 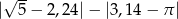 jest równa
jest równa
A) 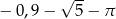 B)
B) 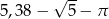 C)
C) 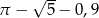 D)
D) 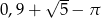
Iloczyn 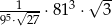 jest równy
jest równy
A) 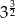 B)
B) 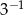 C)
C) 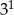 D)
D) 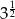
Jeżeli liczba 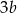 jest o 50% większa od połowy liczby
jest o 50% większa od połowy liczby 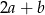 , to liczba
, to liczba  jest większa od
jest większa od 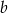 o
o
A) 100% B) 150% C) 50% D) 200%
Zbiór rozwiązań nierówności 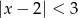 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 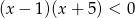
B) 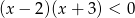
C) 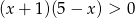
D) 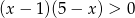
Prosta 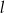 ma równanie
ma równanie 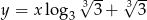 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 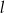 .
.
A) 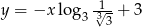
B) 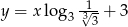
C) 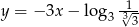
D) 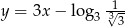
Iloczyn wielomianów 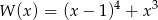 i
i 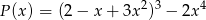 jest wielomianem stopnia
jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7
Punkty 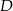 i
i 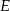 dzielą bok
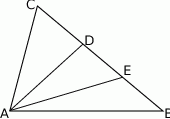
dzielą bok 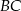 trójkąta
trójkąta 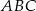 na trzy równe części (zobacz rysunek). Stosunek pól trójkątów
na trzy równe części (zobacz rysunek). Stosunek pól trójkątów 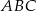 i
i  jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 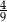
Wykres funkcji 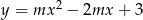 przechodzi przez punkty
przechodzi przez punkty 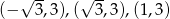 . Wtedy
. Wtedy
A) 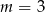 B)
B) 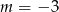 C)
C) 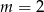 D)
D) 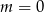
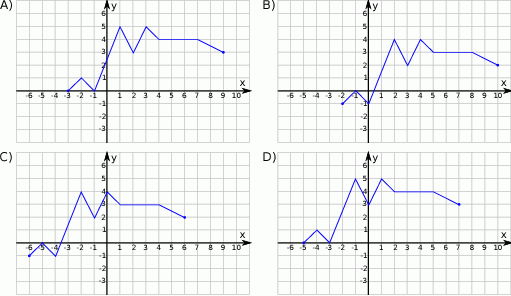
Rysunek przedstawia wykres funkcji 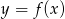 .
.
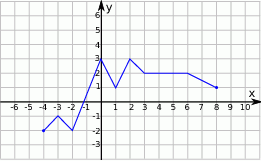
Wskaż wykres funkcji 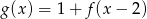 .
.
Wskaż 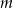 , dla którego funkcja liniowa
, dla którego funkcja liniowa 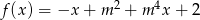 jest malejąca.
jest malejąca.
A) 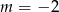 B)
B) 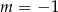 C)
C) 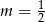 D)
D) 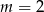
W ciągu arytmetycznym  wyraz
wyraz 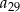 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 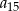 oraz
oraz 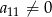 . Wtedy iloraz
. Wtedy iloraz 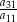 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Liczby 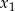 i
i 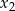 są pierwiastkami równania
są pierwiastkami równania 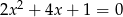 i
i 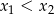 . Oblicz
. Oblicz 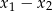 .
.
A) 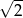 B)
B) 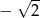 C) -2 D)
C) -2 D) 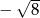
Wartość wyrażenia 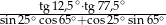 jest równa
jest równa
A) 1 B) 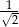 C)
C) 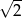 D)
D) 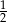
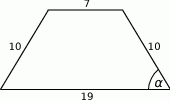
Dany jest trapez równoramienny (patrz rysunek). Wtedy 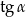 jest równy
jest równy
A) 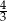 B)
B)  C)
C)  D)
D) 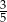
W malejącym ciągu geometrycznym 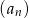 mamy
mamy 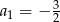 i
i 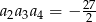 . Iloraz tego ciągu równy
. Iloraz tego ciągu równy
A) 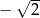 B)
B) 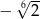 C)
C) 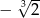 D)
D) 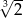
Ciąg 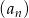 określony jest wzorem
określony jest wzorem 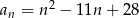 , gdzie
, gdzie 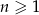 . Liczba niedodatnich wyrazów tego ciągu jest równa
. Liczba niedodatnich wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 7
Wskaż równanie okręgu stycznego do osi 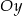 .
.
A) 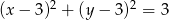
B) 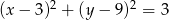
C) 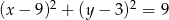
D) 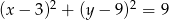
W kwadracie 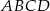 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 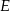 i
i 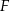 na bokach
na bokach 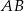 i
i 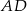 w ten sposób, że odcinek
w ten sposób, że odcinek 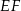 jest równoległy do przekątnej
jest równoległy do przekątnej 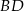 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
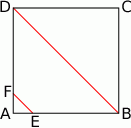
Długość odcinka 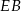 jest równa
jest równa
A) 12 B) 15 C) 14 D) 16
Punkty 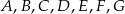 są wierzchołkami siedmiokąta foremnego.
są wierzchołkami siedmiokąta foremnego.
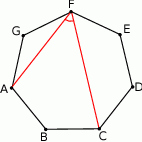
Miara zaznaczonego na rysunku kąta 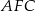 jest równa
jest równa
A) 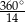 B)
B) 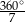 C)
C) 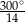 D)
D) 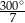
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 58. Ile krawędzi ma ten ostrosłup?
A) 29 B) 14 C) 28 D) 15
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość największej z utworzonych części?
A) 62,5% B) 37,5% C) 65% D) 75%
Zadania otwarte
Wyznacz najmniejszą i największą wartość funkcji 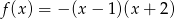 w przedziale
w przedziale 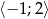 .
.
Rozwiąż równanie 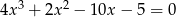 .
.
Długość przeciwprostokątnej trójkąta prostokątnego o obwodzie 90 jest liczbą całkowitą i jest o 1 większa od długości jednej z przyprostokątnych. Oblicz pole tego trójkąta.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 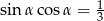 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 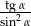 .
.
Odcinki 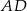 i
i 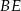 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 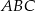 , a punkt
, a punkt 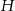 jest punktem ich przecięcia. Uzasadnij, że punkty
jest punktem ich przecięcia. Uzasadnij, że punkty 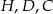 i
i 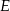 leżą na jednym okręgu.
leżą na jednym okręgu.
Pole koła wpisanego w sześciokąt foremny wynosi 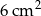 . Oblicz pole koła opisanego na tym sześciokącie.
. Oblicz pole koła opisanego na tym sześciokącie.
Oblicz pole pięciokąta 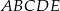 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 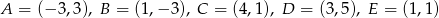 .
.
Linia kolejowa między miastami 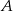 i
i 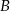 ma długość 711 km. Pociąg jadący z miasta
ma długość 711 km. Pociąg jadący z miasta 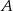 do miasta
do miasta 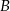 wyrusza 45 minut później niż pociąg jadący z miasta
wyrusza 45 minut później niż pociąg jadący z miasta 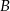 do
do 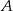 . Pociągi te spotykają się w odległości 450 km od miasta
. Pociągi te spotykają się w odległości 450 km od miasta 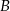 . Średnia prędkość pociągu, który wyjechał z miasta
. Średnia prędkość pociągu, który wyjechał z miasta 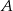 , liczona od chwili wyjazdu z
, liczona od chwili wyjazdu z 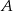 do momentu spotkania, była o 34 km/h mniejsza od średniej prędkości drugiego pociągu liczonej od chwili wyjazdu z miasta
do momentu spotkania, była o 34 km/h mniejsza od średniej prędkości drugiego pociągu liczonej od chwili wyjazdu z miasta 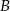 do chwili spotkania. Oblicz średnią prędkość każdego z pociągów w chwili spotkania.
do chwili spotkania. Oblicz średnią prędkość każdego z pociągów w chwili spotkania.
Dany jest graniastosłup prawidłowy czworokątny 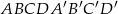 o podstawach
o podstawach 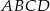 i
i 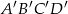 , oraz krawędziach bocznych
, oraz krawędziach bocznych 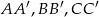 i
i 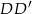 . Oblicz pole trójkąta
. Oblicz pole trójkąta 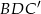 wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem
wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem  , że
, że 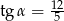 .
.

