/Szkoła średnia/Nierówności/Udowodnij.../Logarytmiczne

Zadanie nr 1387265

Wykaż, że dla dowolnej liczby rzeczywistej 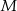M nierówność

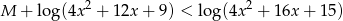
2 2 M + log (4x + 12x + 9) < log (4x + 16x + 15)

ma przynajmniej jedno rozwiązanie w przedziale 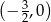( 3 ) − 2,0 .

Wersja PDF

Rozwiązanie

Przekształćmy daną nierówność w sposób równoważny.

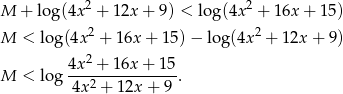
2 2 M + log (4x + 12x + 9) < log (4x + 16x + 15) M < log(4x 2 + 16x + 15)− lo g(4x2 + 12x + 9) 2 M < log 4x--+-16x-+-15-. 4x 2 + 1 2x+ 9

Spróbujmy teraz rozłożyć oba trójmiany. Najpierw licznik

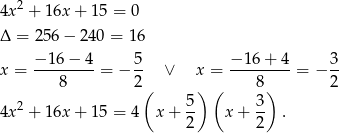
2 4x + 16x + 15 = 0 Δ = 2 56− 240 = 16 x = −-16-−-4-= − 5- ∨ x = −-16-+-4-= − 3- 8 2( ) ( 8) 2 2 5 3 4x + 16x + 15 = 4 x + -- x + -- . 2 2

Teraz mianownik

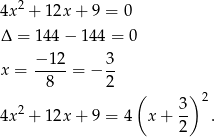
2 4x + 1 2x+ 9 = 0 Δ = 144 − 14 4 = 0 − 12 3 x = -----= − -- 8 2 ( ) 2 3- 2 4x + 1 2x+ 9 = 4 x + 2 .

Nierówność z treści zdania możemy więc zapisać w postaci

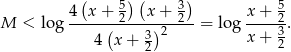
( ) ( ) 4--x-+-52---x-+-32-- x+--52- M < lo g ( 3)2 = log x+ 3. 4 x+ 2 2

Wystarczy teraz zauważyć, że

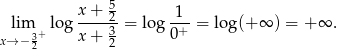
5 lim log x+--2-= log -1- = log(+ ∞ ) = +∞ . x→ −3+ x+ 3 0+ 2 2

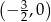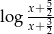To oznacza, że dowolnie blisko lewego końca przedziału ( 3 ) − 2,0 możemy znaleźć argumenty x , dla których 5 log x+-2 x+ 32 przyjmuje dowolnie dużą wartość. To oznacza, że rzeczywiście nierówność

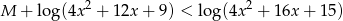
2 2 M + log (4x + 12x + 9) < log (4x + 16x + 15)

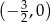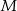ma w przedziale ( ) − 32,0 rozwiązania dla dowolnej wartości M .

Wersja PDF