/Szkoła średnia/Nierówności/Udowodnij.../Logarytmiczne

Zadanie nr 2118493

Wykaż, że jeżeli 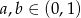a,b ∈ (0,1) to prawdziwa jest nierówność

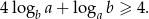
4logb a+ lo gab ≥ 4 .
Wersja PDF

Rozwiązanie

Sposób I

Przekształcamy w sposób równoważny daną nierówność (korzystamy ze wzoru na zmianę podstawy logarytmu).

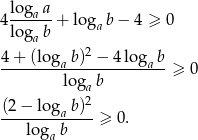
4 lo-gaa-+ log b− 4 ≥ 0 lo gab a 4+ (log b)2 − 4log b --------a-----------a--≥ 0 loga b (2− log b)2 --------a----≥ 0 . loga b

Teraz wystarczy zauważyć, że mianownik jest dodatni (bo 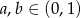a ,b ∈ (0,1) ), a licznik jest nieujemny. Powyższa nierówność jest więc spełniona, a przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musi być spełniona.

Sposób II

Korzystając ze wzoru na zamianę podstawy logarytmu możemy daną nierówność zapisać w postaci

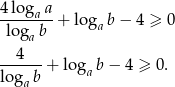
4 lo g a -----a--+ loga b− 4 ≥ 0 logab --4--- log b + lo gab − 4 ≥ 0 . a

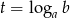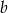Podstawmy teraz t = loga b . Zauważmy, że z podanych założeń o a i b wynika, że t > 0 .

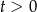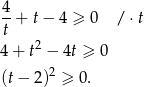
4 --+ t− 4 ≥ 0 / ⋅t t 4 + t2 − 4t ≥ 0 2 (t− 2) ≥ 0.

Otrzymana nierówność jest oczywiście spełniona, więc wyjściowa też musiała być prawdziwa.

Wersja PDF