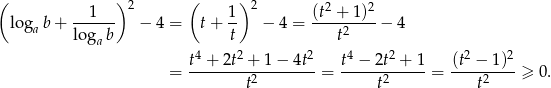Zadanie nr 5759783
Wykaż, że jeżeli 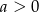 i
i 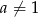 ,
, 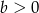 i
i 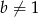 , to
, to 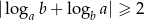 .
.
Rozwiązanie
Obie strony nierówności, którą mamy udowodnić są dodatnie, więc możemy ją stronami podnieść do kwadratu (to najprostszy sposób pozbycia się wartości bezwzględnej) i otrzymamy nierówność
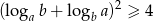
równoważną wyjściowej. Zauważmy jeszcze, że na mocy wzoru na zmianę podstawy logarytmu
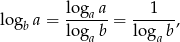
więc nierówność, którą mamy udowodnić jest równoważna nierówności
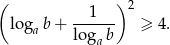
Sposób I
Przekształcamy lewą stronę nierówności.
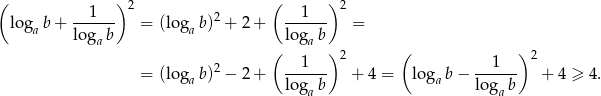
Sposób II
Podstawiamy 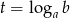 i przekształcamy nierówność.
i przekształcamy nierówność.