/Szkoła średnia/Nierówności/Udowodnij.../Logarytmiczne

Zadanie nr 6904961

Korzystając z tego, że 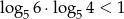log5 6⋅log5 4 < 1 wykaż, że

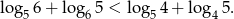
log56 + log 65 < log5 4+ lo g45.
Wersja PDF

Rozwiązanie

Przekształcamy nierówność, którą mamy udowodnić w sposób równoważny. Na początku zamieniamy wszystkie podstawy logarytmów na 5.

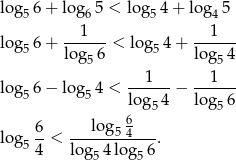
log5 6+ log 65 < log5 4+ lo g45 --1--- ---1-- log5 6+ lo g 6 < lo g54 + log 4 5 5 log 6− log 4 < --1---− ---1-- 5 5 log 54 log 56 6 log 6-< --log-54---. 5 4 log 54 log 56

Ponieważ 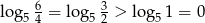lo g 6 = lo g 3 > lo g 1 = 0 54 52 5 , więc możemy podzielić powyższą nierówność stronami przez 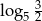3 log5 2 . Otrzymujemy wtedy

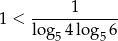
1 1 < ------------ log5 4log5 6

Mianownik liczby z prawej strony jest dodatni, więc nierówność ta jest równoważna nierówności:

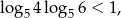
lo g54 lo g56 < 1,

a ta z założenia jest prawdziwa.

Wersja PDF