Zadanie nr 7123678
Zbiór wszystkich liczb  , których odległość od liczby
, których odległość od liczby 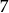 na osi liczbowej jest nie mniejsza niż
na osi liczbowej jest nie mniejsza niż 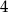 , jest opisany nierównością
, jest opisany nierównością
A) 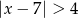 B)
B) 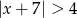 C)
C) 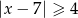 D)
D) 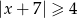
Rozwiązanie
Przypomnijmy, że odległość między dwoma liczbami 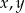 liczymy ze wzoru
liczymy ze wzoru 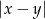 . Zatem odległość między
. Zatem odległość między  i
i 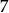 jest równa
jest równa
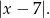
Zauważmy, że skoro odległość między  i
i 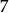 jest nie mniejsza niż
jest nie mniejsza niż 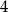 , to znaczy, że jest większa bądź równa
, to znaczy, że jest większa bądź równa 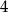 , czyli
, czyli
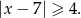
Odpowiedź: C

