Zadanie nr 7471598
Rozwiązaniem nierówności 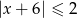 jest zbiór
jest zbiór
A) 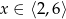 B)
B) 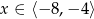 C)
C) 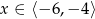 D)
D) 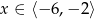
Rozwiązanie
Sposób I
Liczymy
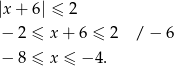
Zatem 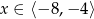 .
.
Sposób II
Daną nierówność możemy zapisać w postaci:
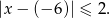
Zatem szukamy tych liczb, które na osi liczbowej są oddalone od 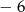 o nie więcej niż 2.
o nie więcej niż 2.
Wykonujemy rysunek
Teraz już łatwo odczytać, że zbiorem rozwiązań jest 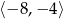 .
.
Odpowiedź: B

