/Studia

Zadanie nr 1019305

Oblicz całkę 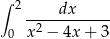∫ 2 dx -2---------- 0 x − 4x + 3 .

Wersja PDF

Rozwiązanie

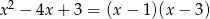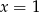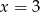Mamy 2 x − 4x + 3 = (x − 1)(x − 3) , zatem funkcja podcałkowa ma dwa punkty osobliwe x = 1 i x = 3 , z których tylko ten pierwszy leży wewnątrz przedziału [0 ,2] . Mamy

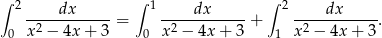
∫ ∫ ∫ 2-----dx----- 1 ----dx------ 2 ----dx------ 0 x 2 − 4x + 3 = 0 x2 − 4x + 3 + 1 x2 − 4x + 3 .

Liczymy całkę nieoznaczoną

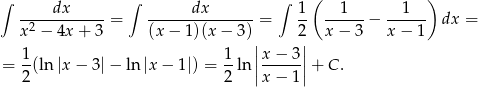
∫ ∫ ∫ ( ) -----dx----- ------dx------- 1- --1--- --1--- x2 − 4x + 3 = (x− 1)(x − 3) = 2 x − 3 − x − 1 dx = | | = 1-(ln |x − 3|− ln |x− 1|) = 1-ln ||x-−-3-||+ C . 2 2 |x − 1 |

W przedziale 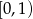[0,1) funkcja podcałkowa ma funkcję pierwotną

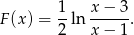
F(x) = 1-ln x-−-3-. 2 x − 1
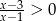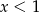Wartość bezwzględną mogliśmy opuścić, bo x−3- x−1 > 0 dla x < 1 . Ponieważ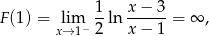
1 x − 3 F(1) = lim --ln ------= ∞ , x→ 1− 2 x − 1
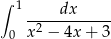więc całka ∫ 1 dx -2---------- 0 x − 4x + 3 jest rozbieżna. Zatem całka 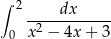∫ 2 dx -2---------- 0 x − 4x + 3 też jest rozbieżna.  
Odpowiedź: Rozbieżna
Wersja PDF