Zadanie nr 1153899
Oblicz całkę 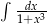 .
.
Rozwiązanie
Ponieważ
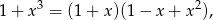
funkcję pod ostatnią całką rozkładamy na ułamki proste postaci
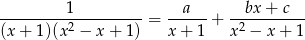
Mnożąc obie strony przez 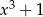 mamy
mamy
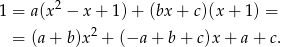
Porównując współczynniki przy kolejnych potęgach  mamy
mamy
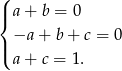
Odejmując od drugiego równania pierwsze i trzecie otrzymamy 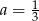 . Zatem
. Zatem 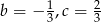 , oraz
, oraz
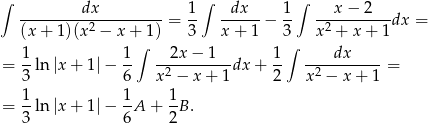
Pierwszą całkę liczymy podstawiając za mianownik, a drugą korzystając ze wzoru
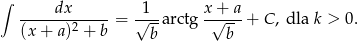
Liczymy
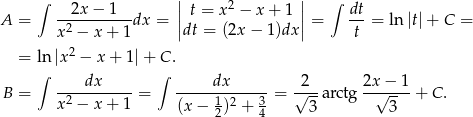
Mamy zatem
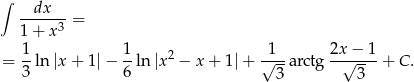
Odpowiedź: