Zadanie nr 1313312
Funkcje 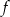 i
i 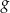 są określone wzorami:
są określone wzorami: 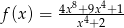 i
i 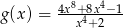 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wykaż, że
. Wykaż, że 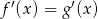 .
.
Rozwiązanie
Sposób I
Mamy wykazać, że
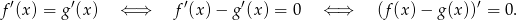
Wystarczy zatem pokazać, że 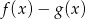 jest funkcją stałą. Sprawdzamy
jest funkcją stałą. Sprawdzamy
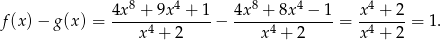
Sposób II
Przekształćmy wzory obu funkcji tak, aby pozbyć się 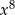 i
i 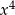 z liczników.
z liczników.
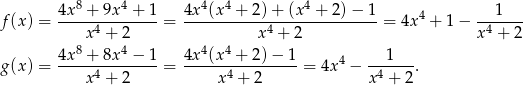
Widać teraz, że 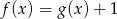 , więc
, więc
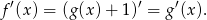
Sposób III
Liczymy pochodną funkcji 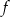 .
.
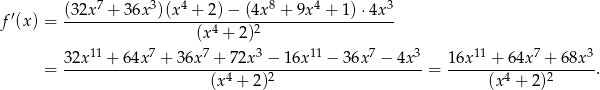
Teraz obliczamy pochodną funkcji 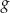 .
.
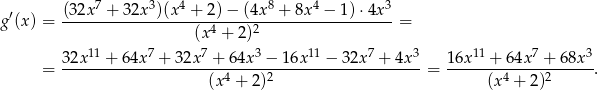
Widać teraz, że rzeczywiście 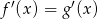 .
.

