Zadanie nr 1415867
Oblicz całkę 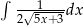 .
.
Rozwiązanie
Sposób I
Ponieważ wyrażenie 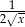 to dokładnie pochodna pierwiastka
to dokładnie pochodna pierwiastka 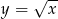 , spodziewamy się wyniku postaci
, spodziewamy się wyniku postaci 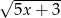 . Jeżeli jednak policzymy pochodną z tego wyrażenia, to otrzymamy z przodu współczynnik 5 pochodzący z pochodnej wnętrza. Zatem dopisujemy z przodu współczynnik
. Jeżeli jednak policzymy pochodną z tego wyrażenia, to otrzymamy z przodu współczynnik 5 pochodzący z pochodnej wnętrza. Zatem dopisujemy z przodu współczynnik 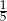 .
.
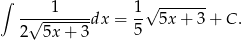
Sposób II
Podstawiamy 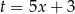 .
.
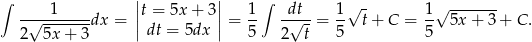
Sposób III
Podstawiamy 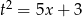 .
.
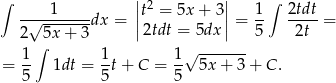
Odpowiedź: