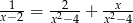Zadanie nr 1447999
Przedstaw funkcję 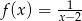 , określoną w zbiorze
, określoną w zbiorze 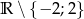 , jako sumę funkcji parzystej i nieparzystej.
, jako sumę funkcji parzystej i nieparzystej.
Rozwiązanie
Musimy znaleźć funkcję parzystą 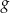 i funkcję nieparzystą
i funkcję nieparzystą 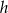 , tak aby
, tak aby
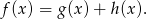
Podstawiając w tej równości 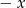 zamiast
zamiast  , mamy
, mamy
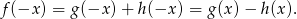
Dodając i odejmując te warunki stronami, mamy
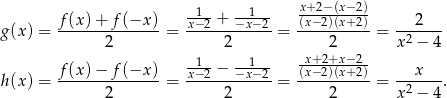
Odpowiedź: