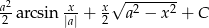Zadanie nr 1579682
Oblicz całkę 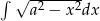 .
.
Rozwiązanie
Sposób I
Podstawiamy 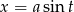 , gdzie
, gdzie ![π- π- t ∈ [− 2,2 ]](https://img.zadania.info/zad/1579682/HzadR1x.gif) . Mamy wtedy
. Mamy wtedy
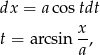
oraz
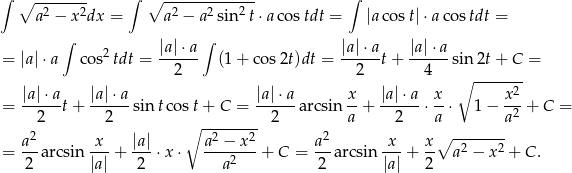
Sposób II
Skorzystamy ze wzoru
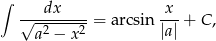
który można łatwo wyprowadzić podstawiając 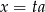 .
.
Przekształcimy teraz szukaną całkę na dwa sposoby: pierwszy z nich to całkowanie przez części, a w drugim przenosimy pierwiastek do mianownika.
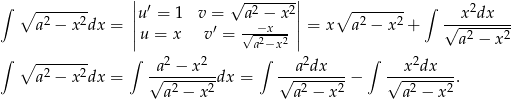
Dodając te dwa wzory stronami otrzymujemy
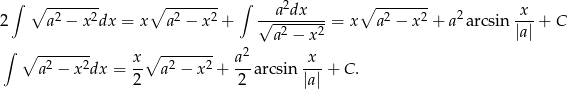
Odpowiedź: