Zadanie nr 1666541
Korzystając ze wzoru 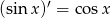 oblicz pochodną funkcji
oblicz pochodną funkcji 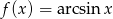 .
.
Rozwiązanie
Sposób I
Różniczkujemy stronami równość
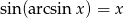
korzystając z podanego wzoru na pochodną sinusa i ze wzoru na pochodną funkcji złożonej.
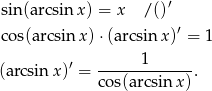
Aby uprościć prawą stronę zauważmy, że jeżeli 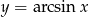 to
to 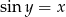 oraz
oraz ![y ∈ [− π-, π] 2 2](https://img.zadania.info/zad/1666541/HzadR4x.gif) . To oznacza, że
. To oznacza, że 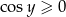 i
i
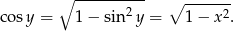
Zatem
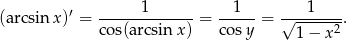
Sposób II
Korzystamy ze wzoru
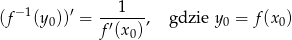
na pochodną funkcji odwrotnej.
Jeżeli oznaczmy 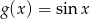 to
to 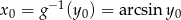 i na mocy powyższego wzoru mamy
i na mocy powyższego wzoru mamy
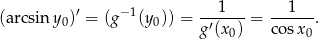
Tak jak w pierwszym sposobie zauważamy, że
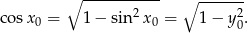
Zatem
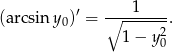
Zamieniając literkę z 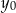 na
na  otrzymujemy
otrzymujemy 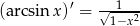 .
.
Odpowiedź: