Zadanie nr 1691933
Wyznacz ekstrema funkcji 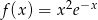 .
.
Rozwiązanie
Liczymy pochodną funkcji.
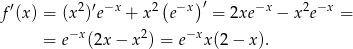
Widać teraz, że znak pochodnej jest taki sam jak znak wyrażenia 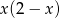 , czyli pochodna jest ujemna w zbiorze
, czyli pochodna jest ujemna w zbiorze 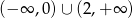 oraz dodatnia w przedziale
oraz dodatnia w przedziale 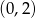 . To oznacza, że funkcja
. To oznacza, że funkcja 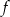 jest malejąca w pierwszym z tych zbiorów i rosnąca w drugim. To z kolei oznacza, że w punkcie
jest malejąca w pierwszym z tych zbiorów i rosnąca w drugim. To z kolei oznacza, że w punkcie 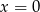 jest minimum lokalne, a w punkcie
jest minimum lokalne, a w punkcie 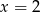 maksimum lokalne.
maksimum lokalne.
Policzmy jeszcze wartości funkcji w tych punktach.
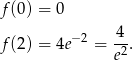
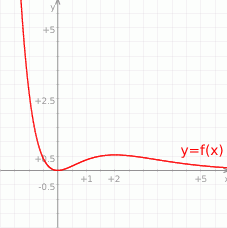
Na koniec obrazek.
Odpowiedź: Minimum lokalne 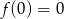 , maksimum lokalne
, maksimum lokalne 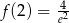 .
.

