Zadanie nr 1889166
Wykazać, że na to aby wektor  był kombinacją liniową wektorów
był kombinacją liniową wektorów 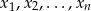 potrzeba i wystarcza aby
potrzeba i wystarcza aby
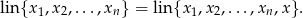
Rozwiązanie
Aby eleganco zapisać rozwiązanie, skorzystamy z implikacji
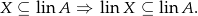
Wynika ona z tego, że 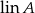 jest podprzestrzenią liniową.
jest podprzestrzenią liniową.
Jeżeli 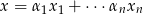 to
to 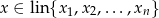 . Zatem
. Zatem
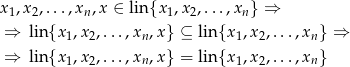
Na odwrót, jeżeli
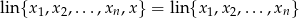
to 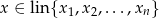 , czyli z definicji
, czyli z definicji 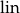 , jest kombinacją liniową wektorów
, jest kombinacją liniową wektorów 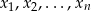 .
.

