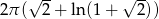Zadanie nr 2018797
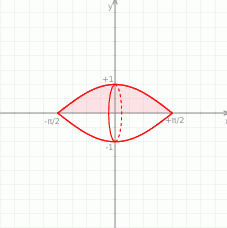
Oblicz pole powierzchni otrzymanej w wyniku obrotu wokół osi 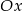 krzywej
krzywej 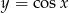 ,
, ![x ∈ [− π2, π2]](https://img.zadania.info/zad/2018797/HzadT2x.gif) .
.
Rozwiązanie
Korzystamy ze wzoru
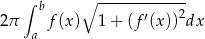
na pole powierzchni otrzymanej przez obrót wokół osi 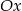 wykresu funkcji
wykresu funkcji 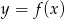 , gdzie
, gdzie ![x ∈ [a,b]](https://img.zadania.info/zad/2018797/HzadR3x.gif) .
.
Liczymy
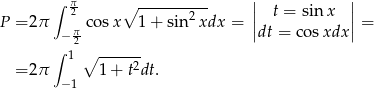
Korzystamy teraz z tego, że całkujemy funkcję parzystą oraz ze wzoru
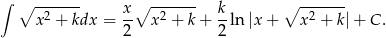
Mamy więc
![∫ 1 ∘ ------ ∫ 1 ∘ ------ 2π 1 + t2dt = 4π 1 + t2dt = − 1 0 [ ∘ ------ ∘ ------] 1 = 4π t- t2 + 1+ 1-ln (t+ t2 + 1) = 2 2 0 ( √ -- √ --) √ -- √ -- = 4π ⋅ --2-+ 1-ln (1+ 2) = 2π ( 2+ ln (1+ 2 )). 2 2](https://img.zadania.info/zad/2018797/HzadR7x.gif)
Odpowiedź: