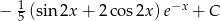Zadanie nr 2283124
Oblicz całkę 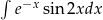 .
.
Rozwiązanie
Będziemy korzystać ze wzoru na całkowanie przez części.
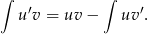
Liczymy (będziemy dwa razy całkować przez części).
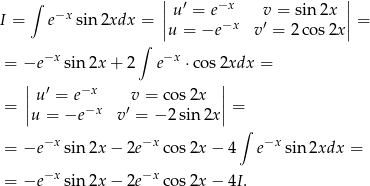
Mamy więc
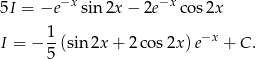
Odpowiedź: 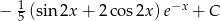
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 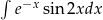 .
.
Będziemy korzystać ze wzoru na całkowanie przez części.
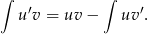
Liczymy (będziemy dwa razy całkować przez części).
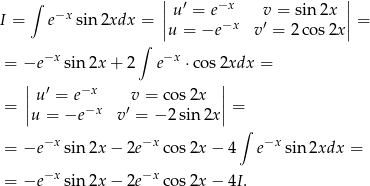
Mamy więc
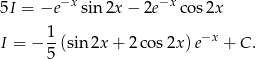
Odpowiedź: