Zadanie nr 2291750
Oblicz całkę 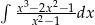 .
.
Rozwiązanie
Liczymy
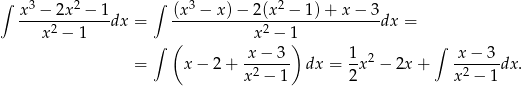
Ostatnią całkę liczymy szukając rozkładu na ułamki proste.
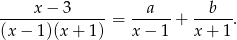
Mnożąc obie strony przez 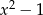 mamy
mamy
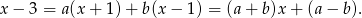
Daje to nam układ równań
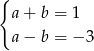
Dodając równania stronami mamy 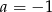 . Stąd
. Stąd 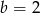 oraz
oraz
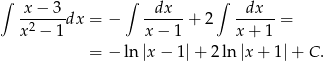
Mamy zatem
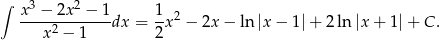
Odpowiedź: 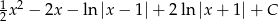
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 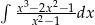 .
.
Liczymy
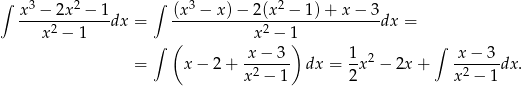
Ostatnią całkę liczymy szukając rozkładu na ułamki proste.
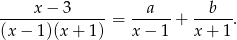
Mnożąc obie strony przez 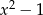 mamy
mamy
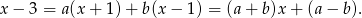
Daje to nam układ równań
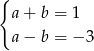
Dodając równania stronami mamy 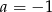 . Stąd
. Stąd 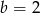 oraz
oraz
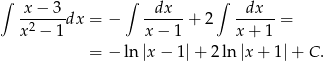
Mamy zatem
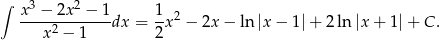
Odpowiedź: